CLASSIFICACIÓ NOMBRES RACIONALS I NOMBRES IRRACIONALS

Nombres racionals 

Anomenem nombre racional el conjunt format per totes les fraccions que són equivalents entre si. Anomenem representant d'un nombre racional qualsevol de les fraccions equivalents que el formen. Cada fracció és un representant d'aquest nombre racional i la fracció irreductible de denominador positiu n'és el representant canònic.

El conjunt de tots els nombres racionals es representa amb Q. Escrivim N inclou Z inclou Q per indicar que el conjunt N dels nombres naturals es troba contingut en el conjunt Z dels nombres enters, i que el conjunt dels nombres enters es troba contingut en el conjunt Q dels nombres racionals. 

Nombres irracionals 

Els nombres decimals no periòdics amb un nombre il·limitat de xifres s'anomenen nombres irracionals. Aquests nombres no es poden escriure en forma de fracció. Els nombres irracionals no pertanyen a cap dels conjunts de nombres que hem estudiat: naturals, enters i racionals. Per tant, sorgeix la necessitat de tornar a ampliar el concepte de nombre, i definir un nou conjunt que incloga tots els tipus de nombres anteriors, però que també continga els nombres irracionals. Aquest nou conjunt és el conjunt dels nombres reals, que estudiarem detalladament a la unitat següent.

FRACCIONS II

En aquesta entrada veurem com multiplicar i dividir fraccions. A diferència de la suma (o resta), aquestes operacions no requereixen que els denominadors siguen iguals.

Finalment, com és d'esperar, el resultat d'aquestes operacions és una fracció, encara que és recomanable escriure la seua forma irreductible (fracció simplificada al màxim), per la qual cosa el resultat pot ser un nombre enter (per exemple, en reduir la fracció 4/2 obtenim l'enter 2).
MULTIPLICACIÓ

El resultat del producte de dues fraccions és la fracció que:

• en el numerador té el producte dels numeradors
• en el denominador té el producte dels denominadors

Exemple (el punt · representa l'operació demultiplicació):

En aquest exemple el resultat ja és irreductible.

Com a regla mnemotècnica solen escriure's les fletxes Paral·leles (Producte) per indicar que els nombres deuen multiplicar-se; per al Quocient (divisió) s'utilitzen les fletxes Creuades.

DIVISIÓ DE FRACCIONS

La divisió de dues fraccions és la fracció que:
el seu numerador és el producte del numerador de la primera fracció i del denominador de la segona
el seu denominador és el producte del denominador de la primera fracció i del numerador de la segona

Exemple (els dos punts : representen la divisió):

FRACCIONS I

Una fracció és una expressió,

,on a i b son nombres enters, b ≠ 0 

Sumes i restes amb fraccions

Com que les fraccions representen nombres (generalment, nombres decimals), té sentit que puguem realitzar operacions entre fraccions: sumar, restar, multiplicar, dividir, etc.

A continuación vorem com sumar i restar fraccions. En les dues operacions distingirem dos casos:

• el denominador de les fraccions és el mateix
• el denominador de les fraccions és distint

En qualsevol cas, no oblidem que sempre hem de simplificar el resultat.

El denominador de les fraccions és el mateix

El denominador es manté. Només hem de sumar els numeradors. 

El denominador de les fraccions és distint

Tant per a sumar com per a restar, si els denominadors de les fraccions no són el mateix, aleshores hem d'aconseguir que ho siguin.

El que farem en aquests casos és escriure una fracció equivalent a cadascun dels sumands. Vegem com:

SUMA

1. Calculem el mínim comú múltiple dels denominadors (factors comuns i no comuns al major exponent).

La descomposició de 14 en nombres primers és: 14=7⋅2

El nombre 7 no es pot descompondre en primers ja que ell mateix és un nombre primer.

Els factors que apareixen en les descomposicions són 2 i 7, tots dos amb exponent 1.

El mínim comú múltiple és el producte de tots els factors al major exponent. Per tant, el mínim comú múltiple de 7 i 14 és

En el denominador de cada fracció escrivim el mínim comú múltiple obtingut:

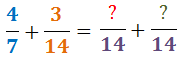
En el numerador de cada fracció escrivim el resultat de dividir el mínim comú múltiple (el nou denominador) entre el denominador inicial i multiplicar-lo pel numerador inicial:

RESTA 

De la mateixa manera que en la suma, fem que els denominadors siguin el mateix:

  

Com que els denominadors són iguals, restem els numeradors:  

NOMBRES RACIONALS I

Un nombre decimal té una part entera, situada a l’esquerra de la coma, i una part decimal, situada a la dretra de la coma.

Tipus de nombres decimals

Els nombres decimals exactes tenen un nombre finit de xifres decimals. Per exemple: 1,34 -5,345 -0,25

Els nombres periòdics purs tenen una part decimal que es repeteix infinitament.

Exemple: 0,6 ≈ 0,666666666666…

Els nombres periòdics mixtos tenen una part no periòdica i a continuació una part periòdica. Exemple: 

Els nombres no exactes i no periòdics no es poden expressar com a fraccions. Exemples:

∏ = 3,14159265.

√2 = ‎1,4142135623731

És possible determinar el tipus de decimal que s'obtindrà a partir de la seua fracció equivalent. Només cal descompondre el denominador en factors:

• Si només està format per factors 2 i/o 5, serà un decimal exacte.

• Si no conté cap 2 i cap 5, serà un decimal periòdic pur.

• Si conté 2 o 5 i altres factors, serà un periòdic mixt.

Qualsevol fracció és pot expressar mitjançant un nombre enter, nombre decimal o nombre decimal periòdic.

NOMBRES IRRACIONALS FAMOSOS

∏	Pi és un nombre irracional famós. S'han calculat més d'un milió de xifres decimals i segueix sense repetir-se. Els primers són aquests: 3,1415926535897932384626433832795 (i segueix ...)
℮	El nombre e (el nombre d'Euler) és un altre nombre irracional famós. S'han calculat moltes xifres decimals d'e sense trobar cap patró. Els primers decimals són: 2,7182818284590452353602874713527 (i segueix ...)
φ	La raó d'or és un nombre irracional. Els seus primers números són: 1,61803398874989484820... (i més...)
√	Moltes arrels quadrades, cúbiques, etc. també són irracionals. Exemples: √3 1,7320508075688772935274463415059 (etc.) √99 9,9498743710661995473447982100121 (etc.) Però √4 = 2, y √9 = 3, ixí que no totes les arrels són irracionals.

Història dels nombres irracionals

Aparentment Hipaso (un estudiant de Pitàgores) va descobrir els nombres irracionals intentant escriure l'arrel de 2 en forma de fracció (es creu que usant geometria). Però en el seu lloc va demostrar que no es pot escriure com a fracció, així que és irracional.

NOMBRES IRRACIONALS

Un nombre irracional és un nombre que no es pot escriure en fracció - el decimal segueix per sempre sense repetir-se.

Exemple: Pi és un nombre irracional. El valor de Pi és:

3,1415926535897932384626433832795 (i més...)

Els decimals no segueixen cap patró, i no es pot escriure cap fracció que tinga el valor Pi.

Nombres com ²²/₇ = 3,1428571428571... s'acosten però no són correctes.

?	Es diu irracional perquè no es pot escriure en forma de raó (o fracció).

Racional o irracional

Però si un nombre, es pot escriure en forma de fracció se l'anomena nombre racional:

Exemple: 9,5 es pot escriure en forma de fracció així

¹⁹/₂ = 9,5

així que no és irracional (és un nombre racional)

Ací tens més exemples:

Nombres	En fracció	Racional o irracional?
5	5/1	Racional
1,75	7/4	Racional
.001	1/1000	Racional
√2 (Arrel quadrada de 2)	?	Irracional!

Exemple: L'arrel quadrada de 2 és un nombre irracional?

La meua calculadora diu que l'arrel de 2 és: 1,4142135623730950488016887242097, però això no és tot! De fet segueix indefinidament, sense que els números es repeteixin.

No es pot escriure una fracció que sigui igual a l'arrel de 2.

Així que l'arrel de 2 és un nombre irracional.

ARREL QUADRADA DE 2

L'arrel quadrada de 2 (o constant pitagòrica) anotada com és definit com l'únic nombre algebraic positiu que, multiplicat per si mateix, dóna el nombre 2, altrament dit, √2 × √2 = 2. És un nombre irracional, que té un valor aproximat de:

1,41242135623

El càlcul del valor aproximat de √2 ha estat un problema matemàtic durant segles. Aquesta recerca ha permès perfeccionar els algorismes de càlcul d'extracció d'arrels quadrades. En informàtica, han servit per optimitzar dels algoritmes en la reducció del temps de càlcul i el consum de memòria

La longitud d'√2 pot ser construïda geomètricament de diverses maneres: per exemple, com la diagonal d'un quadrat de costat la unitat, que és la hipotenusa d'un triangle rectangle isòsceles, val √2 segons el teorema de Pitàgores.

La hipotenusa d'un triangle rectangle isòsceles de costat 1 val √2.

Representació numèrica d'√2.

Amb l'aproximació es pot conèixer un gran nombre de xifres decimals d'aquest número.

L'arrel de dos, també és anomenada constant de Pitàgores en honor al filòsof i matemàtic grec Pitàgores (582 aC - 496 aC), va ser estudiada des de fa molt temps pels babilònics, experts en qüestions de segon grau i disposaven d'un algoritme d'aproximació precís. Des de l'escola de Pitàgores, els grecs del segle V aC i del segle IV aC l'estudien per tal d'entendre millor la incommensurabilitat, concepte equivalent al d'irracionalitat que es coneix actualment. Van trobar fins a tres demostracions diferents de la irracionalitat del nombre, que van conduir a diversos avenços, com el desenvolupament del raonament per l'absurd, el mètode del descens infinit o l'antifèresi, un algoritme comparable a la fracció contínua actual. Per als grecs, ni les fraccions ni els nombres irracionals són nombres. Aquest pas es va donar pels matemàtics àrabs, en el que va ser l'inici a l'àlgebra.

Aquest nombre intervé en diverses aplicacions de la vida quotidiana:

• Per les seues propietats geomètriques, és present en un gran nombre d'obres arquitectòniques. Un exemple d'elles és la Sala Hipòstila del Park Güell de Barcelona, obra de l'arquitecte Antoni Gaudí, on la raó entre la distància entre dues columnes no seguides entre la distància de dues columnes consecutives és igual a l'arrel de dos.
• En astrofísica s'obté que la velocitat mínima que un cos necessita per poder escapar de l'atracció de la gravetat entre la velocitat d'un cos en una òrbita circular és igual a l'arrel de dos.
• Els fulls de paper de format internacional (ISO 216) tenen una proporció entre la llargària i l'amplada igual a l'√2.
• En música, la raó entre les freqüències de la quarta augmentada de l'escala temperada val √2. 
• En electricitat, la tensió màxima del corrent altern monofàsic domèstic val √2 de la tensió eficaç indicada (generalment 110 o 230 V.
• En fotografia, la sèrie de valors d'obertura del diafragma són valors aproximats d'una progressió geomètrica de raó igual a √2.

PASSAR DE DECIMALS A FRACCIONS

Passar de decimals exactes a fraccions

Prenem una fracció que tinga com a numerador el nombre decimal sense la coma i com a denominador la unitat seguida de tants zeros com xifres decimals tinga el nombre.

Exemples:

Expressar el nombre 4,95 en forma de fracció. En el numerador tindrem el número 4,95 sense la coma i en el denominador un 1 seguit de 2 zeros, perquè té 2 decimals: 4,95 = 495/100


Expressar el nombre 0,123456 en forma de fracció: 0,123456 = 123456/100000


Passar de decimals periòdics a fraccions

Per a passar de decimals periòdics mixtos a fraccions es realitza de forma similar. La idea és convertir el decimal periòdic pur multiplicant per la potència de 10 adequada.

Exemple:


Si tenim un nombre periòdic pur, en el numerador s'escriu el nombre sencer sense coma menys la seua part sencera. En el denominador es posa un número amb tants nous com xifres tinga el període.


Expressar el nombre 1,3 periòdic en forma de fracció: ((13-1))/9 = 12/9 = 4/3


(nombre fins al període-nombre abans del període)/(tants "9" com el període i tants "0" com l'anteperíode)

=(138532-1385)/9900 = 137147/9900

RECORDEM...

Prioritat de les operacions

Quan no hi ha parèntesis que ens indiquen quina operació fer primer o en operacions dins d’un parèntesi es va arribar a un acord per saber com actuar. A saber:
1è Es resolen els parèntesis interiors


Si no hi ha parèntesi o dins d’un parèntesi farem:
1è Les potències i les arrels
2è Les multiplicacions i divisions
3é Les sumes i restes
4è Si hi ha diverses operacions amb la mateixa prioritat es faran d’esquerra a dreta.



Ús de parèntesi

Els parèntesis ens indiquen les operacions que s’han de fer primer. Primerament farem els parèntesis interiors i seguirem de dins cap a fora. És com fer un entrepà primer tallem el pa, després decidim el companatge i finalment heu posem dins. És impossible fer-ho al contrari. Per això mira tota l’expressió per veure que es fa primer.
Ha d’haver tants parèntesis oberts com tancats, en cas contrari es diu que “els parèntesis no están ben balancejats”.
Si quelcom multiplica a un parentèsi no cal posar el símbol “.”.
Exemple(3-2)(8-3)= 1x5=5



Operacions amb enters

Regla dels signes per a la suma:

• La suma de 2 nombres positius és positiva. Exemple: +4+8= +12

• La suma de nombres negatius és negativa. Exemple: -5-3= -8
• La suma d’un nombre positiu amb un altre negatiu tindrà el signe major en valor absolut. Exemple: -15+10= -5


Regla dels signes per a la multiplicació i la divisió:
• Positiu x Positiu = Positiu
• Negatiu x Negatiu = Positiu
• Positiu x Negatiu = Negatiu x Positiu = Negatiu